Prediction of the Secondary Arms Spacing Based on Dendrite Tip Kinetics and Cooling Rate
Abstract
:1. Introduction
2. Hypothesis
3. Main Dendrite Tip Kinetic Growth
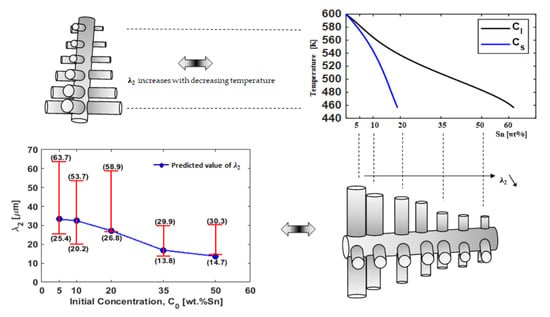
4. Comparison of the Solidification Parameters between Experiment Measurement and Numerical Predictions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| The initial concentration of the alloy | T | Temperature, (K) | |
| C1 | Liquid concentration at r = Rf | TL | Liquidus temperature, (K) |
| Cavr | Average liquid concentration | DT | Thermal gradient, (K/m) |
| Cl*, Cs* | Liquidus and solidus concentrations | Γ | Gibbs Thomson coefficient, (m K) |
| ml | Liquidus slope, (K wt%−1) | rc | The arm radius, (m) |
| Dl | Liquid diffusion coefficient, (m2 s−1) | Rf | The radius of the cylindrical envelope, (m) |
| Ω | Supersaturation | Rtip | The radius of the tip dendrite, (m) |
| UC | Initial undercooling, (K) | V, vtip | Experimental and numerical growth rate of the arm, (m/s) |
| CR | Cooling rate, (K s−1) | σ | The stability constant (σ = 1/4п2) |
| δc | Diffusion distance, (m) | fl, fs | Liquid and solid fractions |
| E1 | The integral exponential function | A | Corrective factor |
| Iv | Ivantsov function | λ 1, λ2 | Primary and secondary dendrite arm spacing, (m) |
| Pe | Peclet number | Vr | Volume of the arm, (m3) |
| pi,qi | constants | Vtot | Total envelope volume, (m3) |
| R | Ideal gas constant, (8.314 J/mol/K) | F | Fitting function |
Appendix A

| Cl (T) | ||||
| −2.9739 10−9 | 6.4158 10−6 | −5.1601 10−3 | 1.8292 | −240.28 |
| Cs (T) | ||||
| 8.5229 10−11 | −2.0961 10−7 | 1.8436 10−4 | −7.0726 10−2 | 10.296 |
Appendix B

| F(Ω) (Equation (A3)) | ||||||
| 11,460 | −8248.5 | 2375.8 | −351.2 | 28.753 | −1.2251 | 0.80449 |
| F(Ω) (Equation (A4)) | ||||||
| 0.19968 | −0.34927 | 0.34839 | 0.020202 | 0.77974 | ||
References
- Steinbach, S.L.; Ratke, L. Effects of controlled convections on dendritic microstructure and segregation during microgravity solidification. In Proceedings of the 18th ESA Symposium on European Rocket and Balloon Programmes and Related Research, ESA-SP 647, Visby, Sweden, 3–7 June 2007; Volume 647, pp. 373–378. [Google Scholar]
- Tewari, S.N.; Shah, R. Macrosegregation During Dendritic Arrayed Growth of Hypoeutectic Pb-Sn Alloys: Influence of Primary Arm Spacing and Mushy Zone Length Mushy Zone Length. Met. Trans. 1996, 27A, 1353–1362. [Google Scholar] [CrossRef]
- Mason, J.T.; Verheoven, J.D.; Trivedi, R. Primary dendrite spacing I. Experimental studies. J. Cryst. Growth 1982, 59, 516. [Google Scholar] [CrossRef]
- Chopra, M.A.; Tewari, S.N. Growth-speed dependence of primary arm spacings in directionally solidified Pb-10 Wt Pct Sn. Met. Trans. 1991, 22A, 2467. [Google Scholar] [CrossRef]
- Klaren, C.M.; Verheoven, J.D.; Trivedi, R. Primary dendrite spacing of lead dendrites in Pb-Sn and Pb-Au Alloys. Met. Trans. A 1980, 11A, 1853. [Google Scholar] [CrossRef]
- Roósz, A.; Rónaföldi, A.; Li, Y.; Mangelinck-Noël, N.; Zimmermann, G.; Nguyen-Thi, H.; Svéda, M.; Veres, Z. Influence of Solidification Parameters on the Amount of Eutectic and Secondary Arm Spacing of Al–7 wt% Si Alloy Solidified under Microgravity. Crystals 2022, 12, 414. [Google Scholar] [CrossRef]
- Roósz, A.; Rónaföldi, A.; Svéda, M.; Veres, Z. Comparison of Dynamical and Empirical Simulation Methods of Secondary Dendrite Arm Coarsening. Crystals 2022, 12, 1834. [Google Scholar] [CrossRef]
- Nikolić, F.; Štajduhar, I.; Čanađija, M. Casting Microstructure Inspection Using Computer Vision: Dendrite Spacing in Aluminum Alloys. Metals 2021, 11, 756. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, M.; Shi, P.; Xu, L. Effects of Alloying Elements on Solidification Structures and Macrosegregation in Slabs. Metals 2022, 12, 1826. [Google Scholar] [CrossRef]
- Ferreira, A.F.; de Castro, J.A.; de Olivé Ferreira, L. Predicting Secondary-Dendrite Arm Spacing of the Al-4.5 wt% Cu Alloy during Unidirectional Solidification. Mater. Res. 2017, 20, 68–75. [Google Scholar] [CrossRef]
- Ramirez-Vidaurri, L.E.; Castro-Román, M.; Herrera-Trejo, M.; Fraga-Chavez, K.-L. Secondary dendritic arm spacing and cooling rate relationship for an ASTM F75 alloy. J. Mater. Res. Technol. 2022, 19, 5049–5065. [Google Scholar] [CrossRef]
- ASTM F75; Standard Specification for Cobalt-28 Chromium-6 Molybdenum Alloy Castings and Casting Alloy for Surgical Implants, ASTM Designation F75-07. American Society for Testing and Materials: West Conshohocken, PA, USA, 2007.
- Üstün, E.; Çadirli, E. Effect of growth rate on coarsening of secondary dendrite arm spacings in directionally solidified of Al-8.8La-1.2Ni ternary alloy. Arch. Metall. Mater. 2022, 67, 931–938. [Google Scholar] [CrossRef]
- Cicutti, C.; Boeri, R. On the relationship between primary and secondary dendrite arm spacing in continuous casting products. Scr. Mater. 2001, 45, 1455–1460. [Google Scholar] [CrossRef]
- Ren, N.; Panwisawas, C.; Li, J.; Xia, M.; Dong, H.; Li, J. Solute enrichment induced dendritic fragmentation in directional solidification of nickel-based superalloys. Acta Mater. 2021, 215, 117043. [Google Scholar] [CrossRef]
- Ren, N.; Li, J.; Bogdan, N.; Xia, M.; Li, J. Simulation of dendritic remelting and fragmentation using coupled cellular automaton and Eulerian multiphase model. Comput. Mater. Sci. 2020, 180, 109714. [Google Scholar] [CrossRef]
- Zheng, Q.-W.; Jing, T.; Dong, H.-B. Modelling of Secondary Dendrite Arms Evolution during Solidification by a Phase-field Method. Mater. Today Proc. 2015, 2, S466–S473. [Google Scholar] [CrossRef]
- Kirkwood, D.H. A simple model for dendrite arm coarsening during solidification. Mater. Sci. Eng. 1985, 73, L1–L4. [Google Scholar] [CrossRef]
- Rappaz, M.; Boettinger, W.J. On dendritic solidification of multicomponent alloys with unequal liquid diffusion coefficients. Acta Mater. 1999, 47, 3205–3219. [Google Scholar] [CrossRef]
- Easton, M.; Davidson, C.; St John, D. Effect of Alloy Composition on the Dendrite Arm Spacing of Multicomponent Aluminum Alloys. Metall. Mater. Trans. A 2010, 41, 1528–1538. [Google Scholar] [CrossRef]
- Ferreira, I.L.; Moreira, A.L.S.; Aviz, J.A.S.; Costa, T.A.; Rocha, O.L.; Barros, A.S.; Garcia, A. On an expression for the growth of secondary dendrite arm spacing during non-equilibrium solidification of multicomponent alloys: Validation against ternary aluminum-based alloys. J. Manuf. Process. 2018, 35, 634–650. [Google Scholar] [CrossRef]
- Sari, I.; Alrasheedi, N.; Ahmadein, M.; Djuansjah, J.; Hachani, L.; Zaidat, K.; Wu, M.; Kharicha, A. Modeling Dendrite Coarsening and Remelting during Directional Solidification of Al-06 wt.%Cu Alloy. Materials 2024, 17, 912. [Google Scholar] [CrossRef]
- Çadirli, E.; Gündüz, M. The directional solidification of Pb-Sn alloys. J. Mater. Sci. 2000, 35, 3837–3848. [Google Scholar] [CrossRef]
- Wu, M.; Li, J.; Ludwig, A.; Kharicha, A. Modeling diffusion-governed solidification of ternary alloys—Part 1: Coupling solidification kinetics with thermodynamics. Comput. Mater. Sci. 2013, 79, 830–840. [Google Scholar] [CrossRef] [PubMed]
- Melendez, M.A.J.; Beckermann, C. Measurements of dendrite tip growth and side branching in succinonitrile-acetone alloys. J. Cryst. Growth 2012, 340, 175–189. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Tran Tech Publications Ltd.: Zurich, Switzerland, 1998. [Google Scholar]
- Wu, M.; Ludwig, A. Modeling equiaxed solidification with melt convection and grain sedimentation—I: Model description. Acta Mater. 2009, 57, 5621–5631. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- McFadden, S.; Browne, D.J. A generalised version of an Ivantsov-based dendrite growth model incorporating a facility for solute measurement ahead of the tip. Comput. Mater. Sci. 2012, 55, 245–254. [Google Scholar] [CrossRef]
- Langer, J.S. Instabilities and pattern forestation in crystal growth. Rev. Mod. Phys. 1980, 52, 1. [Google Scholar] [CrossRef]
- Kharicha, A.; Stefan-Kharicha, M.; Ludwig, A.; Wu, M. A scale adaptive dendritic envelope model of solidification at mesoscopic scales. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 012032. [Google Scholar] [CrossRef]
- Hachani, L.; Zaidat, K.; Saadi, B.; Wang, X.D.; Fautrelle, Y. Solidification of Sn-Pb alloys: Experiments on the influence of the initial concentration. Int. J. Therm. Sci. 2015, 91, 34–48. [Google Scholar] [CrossRef]





| 50% | 35% | 20% | 10% | 5% | C0 | |||||||||||
| 17.11 | 18.45 | 15.29 | 16.36 | 18.58 | Tip Velocity (m/s) ×10−6 | Experimental | ||||||||||
| 0.037 | 0.031 | 0.0254 | 0.0237 | 0.016 | CR (°C/s) | |||||||||||
| 14.7–30.3 | 13.8–29.9 | 26.8–58.9 | 20.2–53.7 | 25.4–63.7 | λ2 (m) ×10−6 | |||||||||||
| 5.3051 | 3.5911 | 2.1144 | 1.2808 | 0.7684 | Under Cooling (K) | |||||||||||
| 17.11 | 18.45 | 15.29 | 16.36 | 18.59 | Tip Velocity (m/s) ×10−6 | Numerical calculation | ||||||||||
| 0.3 | 0.5 | 1 | 0.3 | 0.5 | 1 | 0.3 | 0.5 | 1 | 0.3 | 0.5 | 1 | 0.3 | 0.5 | 1 | A | |
| 08.22 | 13.71 | 27.41 | 10.11 | 16.86 | 33.71 | 16.30 | 27.17 | 54.35 | 19.49 | 32.48 | 64.96 | 19.97 | 33.28 | 66.5 | λ2 predicted (m) ×10−6 | |
| 0.0825 | 0.0932 | 0.0964 | 0.1158 | 0.1507 | Ω | |||||||||||
| 0.0331 | 0.0393 | 0.0412 | 0.0537 | 0.0797 | Pe | |||||||||||
| 1.81 | 2.65 | 4.48 | 6.98 | 10.57 | Rtip (m) ×10−6 | |||||||||||
| 0.469 | 0.622 | 0.831 | 1.063 | 1.237 | D (m2/s) ×10−9 [32] | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sari, I.; Ahmadein, M.; Ataya, S.; Hachani, L.; Zaidat, K.; Alrasheedi, N.; Wu, M.; Kharicha, A. Prediction of the Secondary Arms Spacing Based on Dendrite Tip Kinetics and Cooling Rate. Materials 2024, 17, 865. https://doi.org/10.3390/ma17040865
Sari I, Ahmadein M, Ataya S, Hachani L, Zaidat K, Alrasheedi N, Wu M, Kharicha A. Prediction of the Secondary Arms Spacing Based on Dendrite Tip Kinetics and Cooling Rate. Materials. 2024; 17(4):865. https://doi.org/10.3390/ma17040865
Chicago/Turabian StyleSari, Ibrahim, Mahmoud Ahmadein, Sabbah Ataya, Lakhdar Hachani, Kader Zaidat, Nashmi Alrasheedi, Menghuai Wu, and Abdellah Kharicha. 2024. "Prediction of the Secondary Arms Spacing Based on Dendrite Tip Kinetics and Cooling Rate" Materials 17, no. 4: 865. https://doi.org/10.3390/ma17040865